Instruments de base dans la gestion des risques d'un portefeuille d'options, les lettres grecques, ou “grec(que)s”, sont des outils très utilisés par les traders afin de sécuriser et d’optimiser naturellement leurs plus-values sur les marchés financiers. Que sont les grecques et quelles sont leurs fonctions ? Quels sont les principaux grecs utilisés par les traders ? Voici un résumé complet des informations à connaître pour pouvoir intégrer le suivi des grecques à votre pratique du trading.
Définition des grecques en trading
Rappel sur les options
Une option est un produit dérivé qui donne le droit à son détenteur d’acheter (call) ou de vendre (put) un actif sous-jacent pendant une certaine période et à un prix convenu à l’avance, appelé prix d’exercice. Cet actif peut tout aussi bien être une action qu'un taux de change, une matière première, ou encore une obligation.
Que sont les grecques ?
En mathématiques financières, le pricing d’une option dépend d’un certain nombre de paramètres :
- le prix de l’actif sous-jacent ou spot, noté S ;
- le prix d’exercice, noté K ;
- la date d’échéance de l’option, notée T ;
- le taux d’intérêt, noté R ;
- la volatilité implicite, notée σ.
Issues du modèle d'évaluation des options de Black and Scholes, les grecques servent à calculer l’impact de la variation de ces paramètres sur le prix de l’option. Indispensables dans la gestion des risques des options aussi bien pour les gérants de fonds d'investissement que pour les investisseurs particuliers, les grecs permettent à la fois de mesurer la performance d’un portefeuille d'options et d'analyser l'impact d'un paramètre donné sur le prix de ces dernières.
Quelles sont les principales grecques en trading ?
Les grecques doivent leur nom à l'utilisation récurrente des lettres de l'alphabet grec dans les mathématiques financières. Pour les calculer, posons d’abord les formules suivantes :
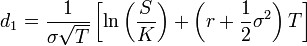 ;
;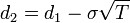 ;
;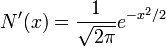 , la loi normale centrée réduite ;
, la loi normale centrée réduite ;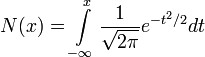 , la fonction de répartition de la loi normale centrée réduite.
, la fonction de répartition de la loi normale centrée réduite.
Le delta
Le delta d'une option mesure la sensibilité de son prix à la fluctuation du prix de l'actif sous-jacent auquel elle est rattachée. Il correspond ainsi à la première dérivée de la valeur de l'option par rapport au prix de l'instrument sous-jacent. En notant P la prime de l’option, on obtient :
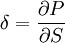
- δCall = N (d1)
- δPut = δCall − 1 = N (d1) − 1
Pour une option vanille, le delta sera un nombre compris entre 0 et 1 pour un call et entre 0 et de -1 pour un put. Plus la valeur du delta est proche de 1 pour un call et -1 pour un put, plus l’option est fortement "dans la monnaie" (ITM). À l'inverse, plus la valeur du delta se rapproche de 0, et plus l'option est "hors de la monnaie" (OTM). Enfin, plus le prix du sous-jacent est élevé pour un call et bas pour un put, plus l’option est chère. À noter que le delta d'un portefeuille d'options est égal à la somme de chacun des deltas des options qui le composent.
Le gamma
Le gamma mesure la convexité du prix d'une option en fonction du cours de son actif sous-jacent. En d’autres termes, si le delta représente la vitesse, le gamma représente l’accélération. Cette lettre indique en effet si le prix d’une option tend à fluctuer plus ou moins rapidement que celui de son sous-jacent, et correspond donc à la dérivée seconde de la fonction de valeur par rapport au prix du sous-jacent.
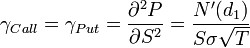
Le gamma est dit long dans le cas d'un achat de call ou de put, et short dans le cas d'une vente. Plus une option se trouve dans la monnaie, et plus la valeur du gamma est importante, car la variation de la valeur du sous-jacent agit fortement sur son delta, et inversement. Comme le delta, le gamma d'un portefeuille d'options est égal à la somme des gammas des options qui le composent.
Le thêta
Le thêta est un indicateur qui représente le coût du temps qui s’écoule sur un portefeuille d’options. En effet, cette grecque mesure l'érosion quotidienne de la valeur d'une option, du simple fait que le temps passe. Ainsi, le thêta d'une option augmente au fur et à mesure de l'avancée de son échéance, l’option enregistrant une perte de valeur exponentielle lorsque son échéance devient inférieure à un mois. Ainsi :
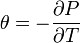
Pour les calls et puts européens sur une action ne versant pas de dividendes, on obtient par ailleurs :
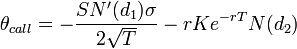 ;
;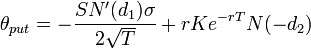 .
.
À noter qu’une position longue au gamma positif aura forcément un thêta négatif. À l'inverse, le thêta est positif pour les vendeurs ou les émetteurs d’options.
Le véga
Selon le modèle de Black and Scholes, le véga mesure la sensibilité d'une option à la volatilité implicite. À l'inverse du gamma et du thêta, cet indicateur est une fonction croissante de la maturité. Par conséquent, les fluctuations de volatilité ont plus d'impact sur les options dont la date d'échéance est éloignée. Un acheteur de call ou de put sera ainsi long véga, et, inversement, un vendeur ou un émetteur d'options sera short véga.

Le rhô
Enfin, le rhô d'une option mesure le taux de variation de la valeur de cette option par rapport au taux d'intérêt sans risque. Il se calcule de la manière suivante :
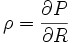
- ρcall = KTe − rTN (d2)
- ρput = − KTe − rTN (− d2)
En résumé, les grecques sont des indicateurs très utilisés pour mesurer les risques des options en isolant différents paramètres influant sur leur prix. Ils sont ainsi d'une aide précieuse pour constituer un portefeuille d'options sûr et performant.